Recently, Pan Jianwei completed the first verification demonstration of Topological Data Analysis (TDA) algorithm on optical quantum computer, which indicates that data analysis may be an important application of quantum computing in the future. Quantum computing has become a State of the weighing, IBM, Google, Microsoft and other companies have layout. But the basic physical problems of quantum computing is still far from settled, such as: reducing the error rate, error rate adaptation and expansion of the scale, it is difficult to extricate themselves from implementation.
Over the past few decades, topology has grown tremendously and has become a powerful tool for analyzing the real world. Simply put, Topology studies the nature of geometry or space that remains constant after continuously changing shapes, such as stretching or bending, but not including tearing or bonding.
In the topological world, symmetry is especially important. Generally speaking, "symmetry" is rotational symmetry, such as changing a square after 90° rotation. However, there is another type of symmetry, which mathematicians refer to as "symmetries persistent homologies". Studying these symmetries is the key to network analysis, data mining, and understanding brain neural network connections.
Continuous coherence (PH) allows us to find ways to characterize the full picture without reducing the dimension. Suppose there is a 100 x 900 array, column (100) is a variety of parameters, and row (900) is a separate data point, stored in an Excel spreadsheet. In the three-dimensional space, we can't describe the whole picture of the data, and the data is represented by the dimension reduction method, which will lose some potentially valuable information. Because topology is mainly concerned with the relationship between points and points in the study of mathematical space properties, the relationship between points and lines (such as distance and angle) is ignored. Therefore, PH allows us to ask topological questions about data in a reliable, non-doped data mining and processing distortion.
The output of the continuous coherence is generally a "barcode" map, which looks like this (bottom):
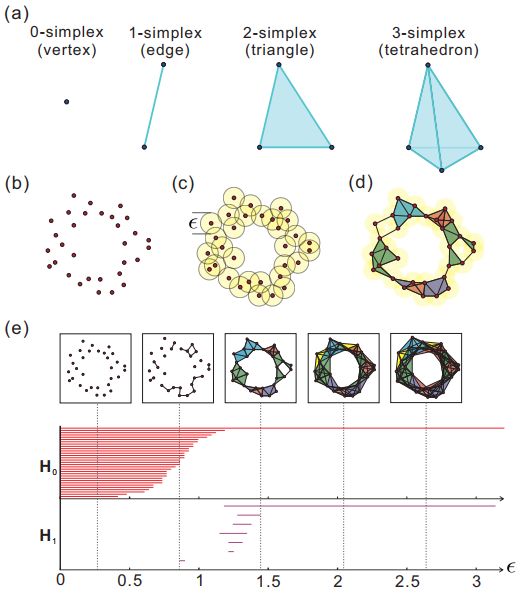
In theory, these symmetries can be characterized by calculating the number of holes and voids in the data structure. The resulting number is called the "Betti number" and the structure with the same Betty number is topologically equivalent.
However, there is a problem. Calculating the Betty number requires a lot of computational power, even if it is only the Betty number of the small data set, it is very expensive for the traditional computer. For this reason, mathematicians have had very limited success in using Betty's numbers to study real-world problems.
However, this issue may be resolved with the implementation of a new study. Recently, a team composed of institutions such as the Chinese University of Science and Technology led by Pan Jianwei and Lu Chaoyang, and the Chinese Academy of Sciences-Alibaba Quantum Computing Laboratory completed the first proof-of-concept for topological data analysis (TDA) on small-scale photon processors. Demo.
The researchers said that their experiments successfully demonstrated the feasibility of the quantum TDA algorithm and showed that data analysis may be an important application for future quantum computing.
The first author of the paper was He-Liang Huang. This demonstration was based on the work of MIT's Seth Lloyd and colleagues. Lloyd et al. developed a quantum algorithm called Topology Data Analysis (TDA) in 2016. Greatly speed up the calculation of the Betty number. The TDA quantum algorithm is spread by the 5th power of n, which is several orders of magnitude faster than the fastest known classical algorithms. However, this research is completely theoretical.
Now, the work done by Huang et al. is to run the TDA algorithm on a quantum computer in a principle verification experiment. The team used a six-photon quantum processor to analyze the topological characteristics of the Betty numbers of three data points in two different scale networks. The results were exactly as expected. The experimental device is as follows:

This provides a completely new approach to analyzing complex data sets. Huang and his colleagues said: "The future of this field will open up new areas for data analysis in quantum computing, including signal and image analysis, astronomy, online and social media analysis, behavioral dynamics, biophysics, oncology. And neuroscience."
Three legs, IBM, Google, Microsoft in the quantum hegemony, effective operation, full firepower
After decades of silence, quantum computing suddenly became hot, excited and active.
About two years ago, IBM provided a quantum computer called IBM Q with 5 qubits. This looks more like a researcher's toy than a serious digital calculation, but 70,000 users worldwide.
Now talk about the upcoming "quantum advantage": quantum computers can perform tasks beyond the means of today's best traditional supercomputers. The whole point of quantum computing is the qubit, not the classical position. For a long time, fifty qubits have been considered to be approximate numbers of quantum computations that can be calculated, and this quantum computation will go through a very long time.
In the past few months, IBM has announced that they have broken through 49 qubit simulations, and Google has been looking forward to a milestone breakthrough. Jens Eisert, a physicist at the Free University of Berlin, said: "The community has a lot of energy and the recent progress is huge.

IBM places quantum computers in large cryogenic vessels (rightmost) that are cooled to above absolute zero.
At the end of January, according to foreign media reports, Google and Microsoft will soon announce a milestone breakthrough in quantum computing technology. In April 2017, Google announced its roadmap for achieving "quantum hegemony", claiming that it will use the 49-qubit simulation system to overcome the problems that traditional computers cannot solve, and will disclose relevant papers in the near future. Microsoft has focused its research and development on "effective maneuvering" and will also announce a major breakthrough in the near future.
It can be seen that the basic problem is solved in principle. The future road of universal quantum computing is now only an engineering problem, but the basic physics problem of quantum computing is still far from being solved, and it is difficult to be freed from implementation.
Even if we are about to pass the milestone in quantum computing, the next year or two may be whether the quantum computer will completely change the real moment of computing. Everything else can be played and there is no guarantee that a big goal can be achieved.
One of the three major problems to be solved: reducing the error rate
The benefits and challenges of quantum computing are inherent in physics, where traditional computers encode and process information into binary digit strings (1 or 0). The role of qubits is the same, except that they can be placed in a superposition of the so-called states 1 and 0, which means that the measurement of qubit states can lead to an answer of 1 or 0 with some clear probability.
In order to perform calculations with many such qubits, they must all be maintained in an interdependent state superposition - a quantum coherent state in which the qubits are said to be entangled. Thus, the adjustment of one qubit may affect all other quanta.
This means that the computational operations for qubits are more than the computational operations for legacy bits. Computational resources increase in proportion to the number of bits in a traditional device, but additional qubits can double the resources of a quantum computer. This is why the difference between a 5-qubit and a 50-qubit machine is very significant.
Quantum computing is so powerful that it is difficult to specify the meaning of quantum mechanics. The equations of quantum theory certainly show that it will work: at least for some categories of calculations, such as decomposition or database search, the calculations have a lot of speed. But what is it?
Perhaps the safest way to describe quantum computing is to say that quantum mechanics in some way creates "resources" for the computations provided by traditional devices.
As Daniel Gottesman, a quantum theorist at the Waterfront Research Institute in Waterloo, Canada, said: "If you have enough quantum mechanics, in a sense, you have acceleration. If not, you don't accelerate. .
In order to perform quantum calculations, you need to keep all the qubits consistent. This is very difficult. The interaction of the quantum coherent entity system with its surroundings creates a channel through which coherence quickly "leaks" out in a process called decoherence.
Researchers looking to build quantum computers must avoid decoherence, which they can only do in a fraction of a second. As the number of qubits increases and the likelihood of interacting with the environment increases, the challenge is growing.
Although quantum computing was first proposed by Richard Feynman in 1982, and the theory was developed in the early 1990s, until now, people began to study devices that could actually make meaningful calculations.
The second root cause of quantum computing is so difficult, just like other natural processes, it is noisy. The heat in the qubits, or random fluctuations from the fundamental quantum mechanical process, occasionally flips or randomizes the state of the qubits, potentially causing computational failure. This is also a danger in traditional computing, but it is not difficult to handle. You only need to keep two or more backup copies of each bit so that the randomly flipped bits behave as odd bits.
Researchers working on quantum computers have developed strategies for how to deal with noise. But these strategies place a huge burden on computational overhead, and all computing power is used to correct errors rather than running algorithms.
Andrew Childs, co-director of the University of Maryland's Joint Center for Quantum Information and Computer Science, said: "The current error rate significantly limits the length of computation that can be performed.
A lot of research in quantum computing is devoted to error correction, which stems from another key feature of quantum systems: as long as the value of quantum bits is not measured, the superposition can only be maintained. If you make a measurement, the overlay will collapse to a certain value: 1 or 0. Then if you don't know what state it is, you can't determine if a qubit is wrong.
A clever solution involves indirect finding, by coupling a qubit to another "parameter" qubit, which does not participate in the calculation, but can be detected without destroying the state of the main quantum itself. Although it is complicated to implement. Such a solution means that to build a true "logic qubit" on which error correction calculations can be performed, many physical qubits are required.
Alán Aspuru-Guzik, a quantum theorist at Harvard University, estimates that today, there are about 10,000 physical qubits that need to be a logical qubit, a completely unrealistic quantum number. He said that if it gets better, this number may drop to thousands or even hundreds.
Eisert is not so pessimistic, saying that the magnitude of 800 physical quantum may be enough, but even so, he thinks that "the overhead is heavy," and now we need to find a way to deal with the error-prone qubit.
Another way to correct errors is to avoid them or to cancel their effects: the so-called error mitigation. For example, IBM researchers are developing a computational method for statistically calculating how many errors can occur in a calculation and then extrapolating the results to a "zero noise" limit.
Some researchers believe that the problem of error correction will become tricky and will prevent quantum computers from achieving their ambitious goals.
Gil Kalai, a mathematician at the Hebrew University in Jerusalem, Israel, said: "The task of making quantum error correction codes is more difficult than displaying quantum advantages." He added, "Devices without error correction are computationally primitive, based on primitives. The advantage is impossible. In other words, when you still have errors, you will never do better than a traditional computer.
Others believe that this problem will eventually be broken. Jay Gambetta, a quantum information scientist at IBM's Thomas J. Watson Research Center, said: "Our recent experiments at IBM have demonstrated the fundamental elements of quantum error correction for small devices, paving the way for large-scale devices for reliable storage of qubits. Quantum information exists in noise for a long time."
Even so, he admits that "a general fault-tolerant quantum computer that must use logical qubits still has a long way to go." He is optimistic about this: "I am sure we will see an experimental demonstration of error correction improvement, but it will take some time."
The three major problems need to be solved: the adaptation error rate, approximate quantum computing
At present, quantum computers are prone to errors, and IBM researchers are discussing the short-term performance of the "approximate quantum computing" field: finding ways to adapt to noise.
This requires algorithms that can tolerate errors, even though they get the right results. Gambetta said: "A quantum computing with sufficient size and high fidelity should have some advantages, even if it is not completely fault tolerant.
The most direct fault-tolerant application seems to be more valuable to scientists than to the whole world: simulating atomic things. (This is actually Feynman's motivation to push quantum computing.) The quantum mechanics equation defines a way to calculate the properties of molecules such as drugs, such as stability and chemical reactivity. However, they cannot be solved classically without a lot of simplification.
Conversely, the quantum behavior of electrons and atoms, Childs said, "is quite similar to the behavior of quantum computers themselves," so an accurate computer model can be constructed. "Many communities, including me, believe that quantum chemistry and materials science will be one of the first useful applications for such devices," Aspuru-Guzik said, and he has been working hard to push quantum computing in this direction.
Quantum simulations have proved their worth even on very small quantum computers available to date. A group of researchers, including Assuru-Guzik, developed an algorithm called the variable component eigenstate (VQE), which effectively finds the lowest energy of a molecule even in the presence of noisy qubits. state.
So far, it can only handle small molecules with very few electrons. These classic computers can already be accurately simulated. But Gambetta and colleagues were getting better and better at IBM in September when they used a 6-qubit device to calculate the electronic structure of molecules including lithium hydride and hydrazine. According to Markus Reiher, a physical chemist at the Federal Institute of Technology in Zurich, Switzerland, this work is "a major leap in quantum systems." Gambetta said: "Using VQE to simulate small molecules is a good example of the feasibility of recent heuristic algorithms.
But even in this application, Assuru-Guzik admits that I will be very excited when the error-corrected quantum computing becomes a reality.
"If we have more than 200 logical qubits, we can go beyond standard methods in quantum chemistry," Reiher added. "If we have about 5,000 such qubits, then quantum computers will change in this area."
The three major problems need to be resolved: the scale of expansion
The rapid growth of quantum computers from 5 to 50 in almost a year has brought hope, but we should not care too much about these numbers because they only tell a part of the story. What matters is how efficient the algorithm is.
Any quantum calculation must be done before the decoherent start and disturb the qubit. Typically, currently assembled qubits have a decoherence time of a few microseconds. The number of logical operations you can perform in a short moment depends on the switching speed of the quantum. If this time is too slow, it doesn't matter how many qubits you can use. The number of operations required for the calculation is called depth: the low depth (shallow) algorithm is more feasible than the high depth algorithm, but the question is whether they can be used to perform useful calculations.
More importantly, not all quantum is the same noisy. In theory, very low noise qubits should be made from the so-called topological electronic states of certain materials, where the electronic state "shape" used to encode the binary information gives a protection against random noise. The most prominent thing for Microsoft researchers is to look for such topological states in exotic quantum materials, but there is no guarantee that they will be discovered or will be controlled.
Researchers at IBM suggest that the ability of quantum computing on a given device is represented as a "quantum volume" number that binds all relevant factors together: the number and connectivity of quantum numbers, the depth of the algorithm, and other measures of the gate. Quality, such as noisy. The power of quantum computing is this quantum volume, and Gambetta says that the best way to do this now is to develop quantum computing hardware to increase the available quantum volume.
This is one of the reasons why the idea of ​​quantum superiority is more feasible than it seems, but it leaves a lot of problems. Which problem to win? How do you know that quantum computers have got the right answer, can you check it with a tried and tested classic device? If you can find the right algorithm, how can you be sure that the traditional machine will not do better?
So quantum advantage is a concept that is handled with care. Some researchers are now more willing to talk about the acceleration provided by quantum devices.
Eisert said: "Proving a clear quantum advantage will be an important milestone, and it will prove that quantum computers can indeed extend the technical possibilities."
This may be more like a symbolic gesture than a useful computing resource conversion. But such things can be important, because if quantum computing is successful, then IBM and Google will not suddenly provide quality new machines. It is achieved through interaction between developers and users, perhaps through messy collaboration, and technology will only develop in the latter when they have enough conviction that the work is worthwhile.
That's why both IBM and Google are keen to provide devices as soon as they are ready. In addition to providing a 16-bit IBM Q experience for anyone registering online, IBM is now also for JP Morgan Chase, Daimler, Honda, Samsung and Oxford. Corporate customers such as universities offer a 20-qubit version. Not only does this help customers discover their content, it should create a programmer's quantum knowledge community that will design resources and solve problems, rather than problems that individual companies may encounter.
Gambetta said: "Quantum computing needs traction and flowering. We must let the world use and learn it."
Lcd Bar Display,Shelf Edge Display,Stretched Bar Lcd,Stretched Bar Display
APIO ELECTRONIC CO.,LTD , https://www.displayapio.com